八大经典排序算法

C语言实现经典排序算法，代码同样在 Visual Studio 2019 上测试过。

时间汇总:

2021.5.24 更新六个排序算法:

1. 直接插入排序；
2. 折半插入排序；
3. 希尔排序；
4. 冒泡排序；
5. 快速排序；
6. 选择排序。

2021.5.25 更新堆排序、归并排序。

具体代码实现请戳我 (opens new window)

结果展示

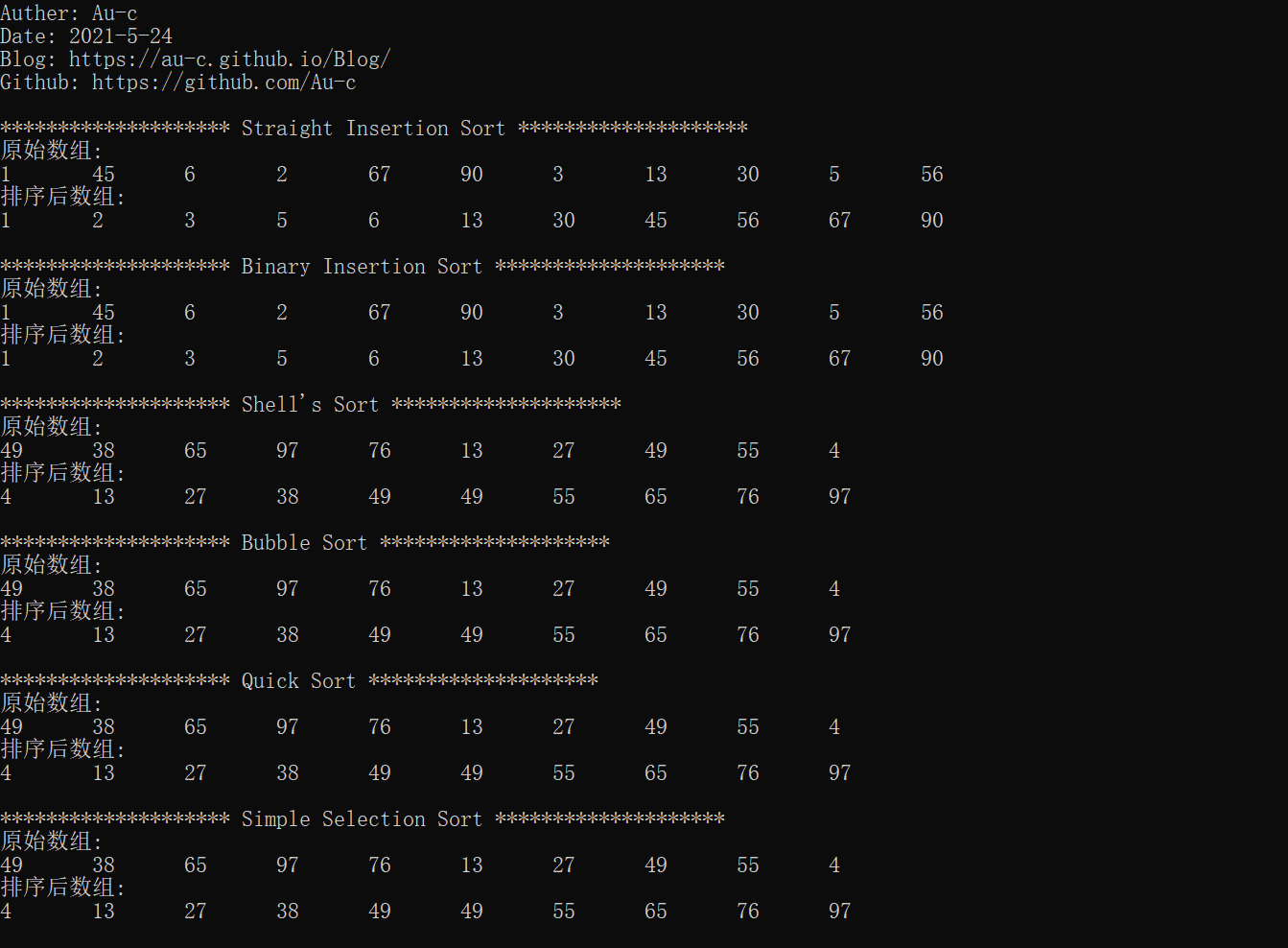
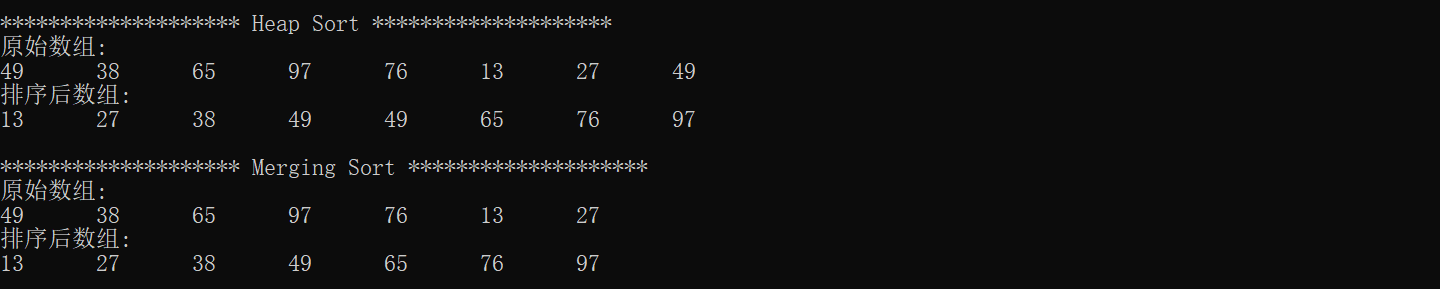
代码

/*
* Auther: Au-c
* Date: 2021-5-25
* Blog: https://au-c.github.io/Blog/
* Github: https://github.com/Au-c
*/

/*
* 简单插入排序
* @param arr {Array} 目标数组
* @param n {int} 元素数量
*/
void InsertSort(ElemType arr[], int n)
{
	int i, j;
	for (i = 2; i <= n; i++)
	{
		arr[0] = arr[i];
		if (arr[0] < arr[i - 1])
		{
			// 前面元素后移
			for (j = i - 1; arr[j] > arr[0]; j--)
			{
				arr[j + 1] = arr[j];
			}
			// 插入当前元素
			arr[j + 1] = arr[0];
		}
	}
}

/*
* 折半插入排序
* @param arr {Array} 目标数组
* @param n {int} 元素数量
*/
void BInsertSort(ElemType arr[], int n)
{
	int i, j, low, high, mid;
	for (i = 2; i <= n ; i++)
	{
		arr[0] = arr[i];
		low = 1;
		high = i - 1;
		while (low <= high)
		{
			mid = (low + high) / 2;
			if (arr[0] < arr[mid]) high = mid - 1;
			else low = mid + 1;
		} // 跳出循环后，high < key < low
		for (j = i - 1; j >= high + 1; j--) arr[j + 1] = arr[j]; // 元素后移
		arr[high + 1] = arr[0];
	}
}

/*
* 希尔排序 - 核心
* @param arr {Array} 目标数组
* @param dk {int} 增量
* @param n {int} 元素数量
*/
void ShellInsert(ElemType arr[], int dk, int n)
{
	int i, j;
	for (i = dk + 1; i <= n; i++)
	{
		if (arr[i - dk] > arr[i])
		{
			arr[0] = arr[i];
			// 元素后移
			for (j = i - dk; j > 0 && arr[j] > arr[0]; j-=dk)
			{
				arr[j + dk] = arr[j];
			}
			arr[j + dk] = arr[0];
		}
	}
}
/*
* 希尔排序
* @param arr {Array} 目标数组
* @param dk {Array} 增量数组
* @param n {int} arr[] 数组长度
* @param t {int} dk[] 数组长度
*/
void ShellSort(ElemType arr[], int dk[], int n, int t)
{
	for (int i = 0; i < t; i++)
	{
		ShellInsert(arr, dk[i], n);
	}
}

/*
* 冒泡排序
*/
void BubbleSort(ElemType arr[], int n)
{
	int i, j, flag;
	for (i = 1; i <= n; i++)
	{
		flag = 0;
		for (j = 1; j <= n - i; j++) {
			if (arr[j] > arr[j + 1])
			{
				// 两两交换
				arr[0] = arr[j];
				arr[j] = arr[j + 1];
				arr[j + 1] = arr[0];
				flag = 1;
			}
		}
		if (flag == 0) break;
	}
}

/*
* 快速排序 - 核心: 枢轴默认为首元素
*/
int Partition(ElemType arr[], int low, int high)
{
	arr[0] = arr[low];
	while (low < high)
	{
		while (low < high && arr[high] >= arr[0]) --high;
		arr[low] = arr[high];
		while (low < high && arr[low] <= arr[0]) ++low;
		arr[high] = arr[low];
	}
	arr[low] = arr[0];
	return low;
}
/*
* 快速排序
* @param arr {Array} 目标数组
* @param low {int} 排序区段首元素索引
* @param high {int} 排序区段末尾元素索引 
*/
void QuickSort(ElemType arr[], int low, int high)
{
	if (low < high) 
	{
		int pivotloc = Partition(arr, low, high);
		QuickSort(arr, low, pivotloc - 1);
		QuickSort(arr, pivotloc + 1, high);
	}
}

/*
* 选择排序
* @param arr {Array} 目标数组
* @param n {int} 元素数量
*/
void SelectSort(ElemType arr[], int n)
{
	int i, j, min;
	// 最后剩下一元素无需比较
	for (i = 1; i < n; i++)
	{
		min = i;
		for (j = i + 1; j <= n; j++)
		{
			if (arr[j] < arr[min]) min = j;
		}
		if (min != i)
		{
			// 两两交换
			arr[0] = arr[i];
			arr[i] = arr[min];
			arr[min] = arr[0];
		}
	}
}

/*
* 调整堆 (大根堆)
* @param arr {Array} 目标数组
* @param s {int} 当前子树根节点索引
* @param n {int} 元素数量
*/
void HeapAdjust(ElemType arr[], int s, int n)
{
	int i;
	arr[0] = arr[s];
	for (i = 2 * s; i <= n; i *= 2)
	{
		// 如果左孩子数值更大
		if (i < n && arr[i] < arr[i + 1]) ++i;
		// 如果根节点更大
		if (arr[0] > arr[i]) break;
		// 调整
		arr[s] = arr[i];
		s = i;
	}
	arr[s] = arr[0];
}

/*
* 创建堆 (大根堆)
* @param arr {Array} 目标数组
* @param n {int} 元素数量
*/
void CreatHeap(ElemType arr[], int n)
{
	for (int i = n / 2; i > 0; i--)
	{
		HeapAdjust(arr, i, n);
	}
}

/*
* 堆排序 (大根堆)
* @return 使用场景：1. 每次把首元素输出，从大到小；2. 排序后的数组：一个从小到大的序列
* @param arr {Array} 目标数组
* @param n {int} 元素数量
*/
void HeapSort(ElemType arr[], int n)
{
	// 创建堆
	CreatHeap(arr, n);
	for (int i = n; i > 1; i--)
	{
		// 交换根节点与 arr[i]
		int temp = arr[1];
		arr[1] = arr[i];
		arr[i] = temp;
		// 堆调整
		HeapAdjust(arr, 1, i - 1);
	}
}

/*
* 归并排序 - 核心
* @param arr {Array} 目标序列
* @param low {int} 左序列起始元素索引
* @param mid {int} 划分左右序列的分界: mid 作为左序列末尾元素索引, mid+1 作为右序列起始元素索引
* @param high {int} 右序列末尾元素索引
*/
void Merge(ElemType arr[], int low, int mid, int high)
{
	ElemType* s = (ElemType*)malloc((high - low + 1) * sizeof(ElemType));
	int i = low;
	int j = mid + 1;
	int k = 0;
	for (k; i <= mid && j <= high; k++)
	{
		if (arr[i] <= arr[j]) s[k] = arr[i++];
		else s[k] = arr[j++];
	}
	while (i <= mid) s[k++] = arr[i++];
	while (j <= high) s[k++] = arr[j++];

	for (i = low, k = 0; k < (high - low + 1); i++, k++)
	{
		arr[i] = s[k];
	}
	free(s);
}

/*
* 归并排序
* @param arr {Array} 目标序列
* @param low {int} 左序列起始元素索引
* @param high {int} 右序列末尾元素索引
*/
void MergeSort(ElemType arr[], int low, int high)
{
	if (low < high)
	{
		int mid = (low + high) / 2;
		MergeSort(arr, low, mid);
		MergeSort(arr, mid + 1, high);
		Merge(arr, low, mid, high);
	}
}